
- #4 bit half adder truth table 64 bits#
- #4 bit half adder truth table full#
- #4 bit half adder truth table plus#
This unwanted delay time is called Propagation delay.
#4 bit half adder truth table 64 bits#
However, when the size of the bits is larger for example 32 or 64 bits used in multi-bit adders, or summation is required at a very high clock speed, this delay may become prohibitively large with the addition processes not being completed correctly within one clock cycle. When the size of the bits being added is not too large for example, 4 or 8 bits, or the summing speed of the adder is not important, this delay may not be important. Consequently, there will be a finite delay before the output of the adder responds to any change in its inputs resulting in a accumulated delay.
#4 bit half adder truth table full#
One main disadvantage of “cascading” together 1-bit binary adders to add large binary numbers is that if inputs A and B change, the sum at its output will not be valid until any carry-input has “rippled” through every full adder in the chain because the MSB (most significant bit) of the sum has to wait for any changes from the carry input of the LSB (less significant bit).

An example of a 4-bit adder is given below.
#4 bit half adder truth table plus#
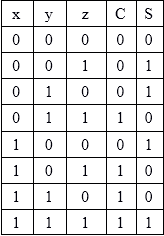
The second binary adder in the chain also produces a summed output (the 2nd bit) plus another carry-out bit and we can keep adding more full adders to the combination to add larger numbers, linking the carry bit output from the first full binary adder to the next full adder, and so forth. It is called a ripple carry adder because the carry signals produce a “ripple” effect through the binary adder from right to left, (LSB to MSB).įor example, suppose we want to “add” together two 4-bit numbers, the two outputs of the first full adder will provide the first place digit sum ( S) of the addition plus a carry-out bit that acts as the carry-in digit of the next binary adder. But what if we wanted to add together two n-bit numbers, then n number of 1-bit full adders need to be connected or “cascaded” together to produce what is known as a Ripple Carry Adder.Ī “ripple carry adder” is simply “ n“, 1-bit full adders cascaded together with each full adder representing a single weighted column in a long binary addition. We have seen above that single 1-bit binary adders can be constructed from basic logic gates. Then the Boolean expression for a full adder is as follows.ĬARRY-OUT = A AND B OR Cin(A XOR B) = A.B + Cin(A ⊕ B) An n-bit Binary Adder Binary Addition of Two Bits 0Īs the full adder circuit above is basically two half adders connected together, the truth table for the full adder includes an additional column to take into account the Carry-in, C IN input as well as the summed output, S and the Carry-out, C OUT bit. So when adding binary numbers, a carry out is generated when the “SUM” equals or is greater than two (1+1) and this becomes a “CARRY” bit for any subsequent addition being passed over to the next column for addition and so on.

Binary Additionīinary Addition follows these same basic rules as for the denary addition above except in binary there are only two digits with the largest digit being “1”. The adding of binary numbers is exactly the same idea as that for adding together decimal numbers but this time a carry is only generated when the result in any column is greater or equal to “2”, the base number of binary. This carry is then added to the result of the addition of the next column to the left and so on, simple school math’s addition, add the numbers and carry. When each column is added together a carry is generated if the result is greater or equal to 10, the base number. From our maths lessons at school, we learnt that each number column is added together starting from the right hand side and that each digit has a weighted value depending upon its position within the columns.


 0 kommentar(er)
0 kommentar(er)
